Ros 下的三轮全向小车

发表于 | 分类于 |

之前写的 这篇文章 分析了三轮全向小车的运动，今天把尝试它部署到 Ros 上。

基本原理

参考系的定义需要根据 Ros by Example chapter 7 做一些修改：

  • 定义三轮车的三个轮子分别是 A、B、C， 速度分别是a、b、c；
  • 定义半径 Radius 是中点到轮子的距离；
  • 定义 a，b 为前轮，c 为后轮。

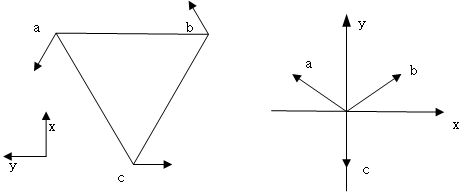
三个速度平移到一点，三个速度大小分别是 a，b，c，分解到坐标系上的坐标应该是：
$$
\overrightarrow{V_a}=(-\frac{\sqrt{3}}{2}a,\frac{1}{2}a)\\
\overrightarrow{V_b}=(\frac{\sqrt{3}}{2}b,\frac{1}{2}b)\\
\overrightarrow{V_c}=(0,-c)
$$
和向量是：
$$
\overrightarrow{S}=(\frac{\sqrt{3}}{2}b-\frac{\sqrt{3}}{2}a,-c+\frac{1}{2}a+\frac{1}{2}b)
$$

以车的旋转中心为车的中心，角速度的计算公式：

$$
\omega=\frac{a+b+c}{3r}
$$

控制程序

Ros 中的的速度消息是 Twist 指定的

1
2
3
4
5
6
7
8
9
$ rosmsg show geometry_msgs/Twist
geometry_msgs/Vector3 linear
  float64 x
  float64 y
  float64 z
geometry_msgs/Vector3 angular
  float64 x
  float64 y
  float64 z

linear 中的 x 代表前进的速度，单位是 m/s 。angular 中的 z 表示角速度，单位 rad/s。

按照这个思路，Twist 消息一般提供 x y z ，需要通过这三个量反解出三个轮子所需要的速度：
$$
\begin{bmatrix}V_x \\ V_y \\ \omega\end{bmatrix}=
\begin{bmatrix}
\frac{-\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & 0\\
\frac{1}{2} & \frac{1}{2} & -1\\
\frac{1}{3r} & \frac{1}{3r} & \frac{1}{3r}
\end{bmatrix}
\begin{bmatrix}a\\ b \\ c \end{bmatrix}
$$
先对矩阵求逆：
$$
\begin{bmatrix}
-\frac{\sqrt{3}}{2} & \frac{\sqrt{3}}{2} & 0\\
\frac{1}{2} & \frac{1}{2} & -1\\
\frac{1}{3r} & \frac{1}{3r} & \frac{1}{3r}
\end{bmatrix}^{-1}=
\begin{bmatrix}
-\frac{\sqrt{3}}{3} & \frac{1}{3} & r \\
\frac{\sqrt{3}}{3} & \frac{1}{3} & r \\
0 & -\frac{2}{3} & r
\end{bmatrix}
$$
带入左式：
$$
\begin{bmatrix}a\\ b \\ c \end{bmatrix}=
\begin{bmatrix}
-\frac{\sqrt{3}}{3} & \frac{1}{3} & r \\
\frac{\sqrt{3}}{3} & \frac{1}{3} & r \\
0 & -\frac{2}{3} & r
\end{bmatrix}
\begin{bmatrix}V_x\\ V_y\\ \omega\end{bmatrix}
$$
python 实现，由于小车没有编码器，只写一个发布速度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#!/usr/bin/env python
# -*- coding: utf-8 -*-

import rospy
from geometry_msgs.msg import Twist
from math import sqrt
import RPi.GPIO as GPIO
import time
import sys

Radius = 10 #圆盘半径，需要根据情况修改

PWMA = 18
AIN1 = 22
AIN2 = 27

PWMB = 23
BIN1 = 25
BIN2 = 24

PWMC = 16
CIN1 = 20
CIN2 = 21

GPIO.setwarnings(False) 
GPIO.setmode(GPIO.BCM)

GPIO.setup(AIN2,GPIO.OUT)
GPIO.setup(AIN1,GPIO.OUT)
GPIO.setup(PWMA,GPIO.OUT)

GPIO.setup(BIN1,GPIO.OUT)
GPIO.setup(BIN2,GPIO.OUT)
GPIO.setup(PWMB,GPIO.OUT)

GPIO.setup(CIN1,GPIO.OUT)
GPIO.setup(CIN2,GPIO.OUT)
GPIO.setup(PWMC,GPIO.OUT)

A_Motor= GPIO.PWM(PWMA,100)
A_Motor.start(0)

B_Motor = GPIO.PWM(PWMB,100)
B_Motor.start(0)

C_Motor = GPIO.PWM(PWMC,100)
C_Motor.start(0)

def compute(Vx,Vy,omega):
    a = -sqrt(3)/3 * Vx + 1/3 * Vy + omega * Radius
    b =  sqrt(3)/3 * Vx + 1/3 * Vy + omega * Radius
    c =                 - 2/3 * Vy + omega * Radius
       
    return a,b,c 

def move(va,vb,vc,t_time = 4):
    A_Motor.ChangeDutyCycle(abs(va))
    GPIO.output(AIN1,bool(va<0))
    GPIO.output(AIN2,bool(va>0))

    B_Motor.ChangeDutyCycle(abs(vb))
    GPIO.output(BIN1,bool(vb<0))
    GPIO.output(BIN2,bool(vb>0))
    
    C_Motor.ChangeDutyCycle(abs(vc))
    GPIO.output(CIN1,bool(vc<0))
    GPIO.output(CIN2,bool(vc>0))

    time.sleep(t_time)

def callback(msg):
    rospy.loginfo("Received a /cmd_vel message!")
    rospy.loginfo("Linear Velocity: [%f, %f, %f]"%(msg.linear.x, msg.linear.y, msg.linear.z))
    rospy.loginfo("Angular Velocity: [%f, %f, %f]"%(msg.angular.x, msg.angular.y, msg.angular.z))

    # 速度获取
    omega = msg.angular.z #角速度
    Vx = msg.linear.x
    Vy = msg.linear.y

    va,vb,vc = compute(Vx, Vy, omega)
    
    rospy.loginfo("va: %f, vb: %f, vc: %f]"%(va, vb, vc))

    move(va,vb,vc)

def listener():
    rospy.init_node('vel_listener')
    rospy.Subscriber('/cmd_vel', Twist, callback)
    rospy.spin()

if __name__ == "__main__":
    try:
        listener()
    except KeyboardInterrupt:
        GPIO.cleanup()